The XYZ color space
Under normal lighting conditions, the cone cells in the retina take care of reproducing colors. There are three kinds of cone cell, with distinct responses to the spectrum. The responses are called The color matching functions.

A linear vector space can be spanned by these three matching functions with inner product
The matching functions then act as a basis, and are called \(\bar{x}\), \(\bar{y}\), and \(\bar{z}\), with \(\bar{x} \cdot \bar{x} = \bar{y} \cdot \bar{y} = \bar{z} \cdot \bar{z}\). The linear vector space is called the CIE XYZ color space. Given a kind of light, its corresponding power spectrum \(p(\lambda)\) is a vector in this space (sort of, if we ignore the dimension), the component of the color of the light are then
As an example, consider an ideal monochromatic light \(q(\lambda) = A\delta(\lambda - \lambda_0)\) with wavelength \(\lambda_0\), in which \(\delta\) is the Dirac delta function. Its X component is
If \(\lambda_0\) is at where the red cone cell is insensitive, for example, 500 nm, \(\bar{x}(\lambda_0)\) is a very small number, and therefore X ≪ A, as expected.
The chromaticity x, y, and z are defined as dimension-less variables
Note that mathematically, \(\bar{x}\), \(\bar{y}\), and \(\bar{z}\) are linearly independent; however, because of their physical interpretation, they are cross-constrained. For example for any given light, if x is large, y cannot be zero, because of the overlap between \(\bar{x}(\lambda)\) and \(\bar{y}(\lambda)\). For this reason, the domain of all possible physical light does not occupy the entire xy-plane. As shown in fig. [The chromaticity line], all visible monochromatic light form the curve, which encloses the domain of all physical visible colors.

There are many chromaticity line plots online, that are filled with a color palette. I believe for most of them, the colors are just some simple gradient pattern, and are not reliable. The color should be calculated carefully based on the value of x, y, and z.
The RGB color space
An RGB color space is spanned by a set of red, green, and blue. The definition of those colors is specific to each RGB space. Fig. [The RGB color space] shows a linear RGB space “embedded” in the xyz space.
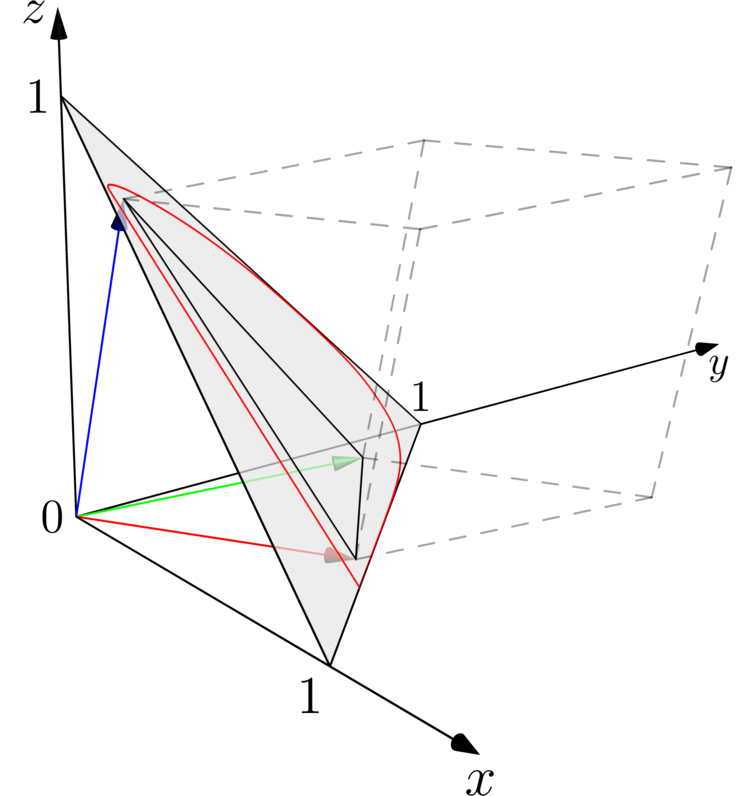
The red, green, and blue vector coincides with those of sRGB and Rec.709 under “white point D65”. The big grey triangle is the \(x+y+z = 1\) plane. The chromaticity line is drawn as the red curve. If one projects it onto the x-y plane, one recovers the curve in fig. [The chromaticity line]. The RGB vectors defines a triangle (shown in black, the smaller one) on the \(x+y+z = 1\) plane; this is the gamut of the RGB color space. The light grey dashed lines visualize the entirety of the linearized version of the RGB color space, inside which are all the colors that can be expressed with this linearized RGB color space.
The sRGB space
Color space sRGB is widely used as a “standard” space on the web. When a program doesn’t support color management, it usually assumes that all the colors it needs to display are in sRGB (I’m looking at you, Chrome). However, professionally sRGB is almost never used in any production workflow, because of its limited gamut. Therefore it is important to know that sRGB is, and how to convert other space from/to it.
The basis vector and gamut of sRGB is shown in Fig. [The RGB color space]. It is then easy to find that there is a linear transformation between linearized sRGB and XYZ:
However the regular sRGB has a nonlinear gamma map to the linearized version shown in the figure:
in which \(a = 0.055\). Note that this map contains a linear section at dark region, and a power law section at the rest of the domain. Therefore, if one wants to convert a color from sRGB to XYZ, one needs to first use the nonlinear map to convert the sRGB color to linearized sRGB, and use the linear transformation to convert it to XYZ. One can use the following ImageMagick command to achieve this:
convert -alpha off -fx "p <= 0.04045 ? p / 12.92 : ((p + 0.055) / 1.055) ^ 2.4" \ -color-matrix "0.4124564 0.3575761 0.1804375 0.2126729 0.7151522 0.0721750 0.0193339 0.1191920 0.9503041" \ -evaluate multiply 0.9166 -gamma 2.6 \ # -depth 12 -quality 0 \ src dest
A very useful scenario in which this command is useful is when one want to convert frames of a movie in sRGB to DCI format, which is are JPEG 2000 files in XYZ space. However if one use any encoder (for example FFmpeg) to encode the frames back to video (and thus convert color space back to sRGB), one will find that the color is wrong in comparison to the original frames. This is because even though sRGB utilizes the multi-section nonlinear map mentioned previously, major video editing softwares like Premiere and Vegas only use a lazy approximate version, which is a simple power law with \(\gamma = 2.6\) across the whole domain. Therefore encoders have to use this map to linearize sRGB in order to achieve consistent color. Thus the ImageMagick command can be simplified to
convert -alpha off -gamma 0.4545454545 \ -color-matrix "0.412390799265959 0.357584339383878 0.180480788401834 0.212639005871510 0.715168678767756 0.072192315360734 0.019330818715592 0.119194779794626 0.950532152249661" \ -evaluate multiply 0.91655527974 -gamma 2.6 \ # -depth 12 -quality 0 \ src dest